By Yifan Zhang
Speakers have quickly become an essential, everyday part of life—from phones, to cars, to theaters, sound surrounds us.
To first understand speakers, we need to understand sound. Sound waves can be categorized based on their shape, or wave forms. Transverse waves are waves where “…the displacement of every such oscillating string element is perpendicular to the direction of travel of the wave” (Halliday et al., 2005). Conversely, longitudinal waves are waves which move air parallel to the direction of travel, and sound waves are an example of longitudinal waves. The movement of a speaker’s diaphragm is what produces the sound waves and can be likened to the movement of a piston. For example, imagine a piston located at the left end of a long pipe, completely sealing it. If it was pushed right and then pulled left, it would send a pulse of sound through the pipe. The movement right pushes on the air particles next to the piston, increasing air pressure next to and away from the piston. The movement left decreases the air pressure next to the piston, so the air particles next to the piston move left. This change in pressure will move rightwards down the pipe, creating a pulse (Halliday et al., 2005).
There are two types of speakers, one being are dynamic speakers, which use a magnet to produce sound waves, and the other being electrostatic speakers, which use oscillating electric currents instead of magnets. Dynamic speakers can be classified into two categories: bass speakers (also known as woofers), and tweeters. Bass speakers and tweeters have the same inner structure but differ in the shape of the diaphragm and the size of the speaker. Because bass speakers produce lower sounds, they have a cone-shaped diaphragm and are larger, while tweeters have a dome-shaped diaphragm and are smaller, improving production of higher pitches. The inner structure of both bass speakers and tweeters relies on electromagnetic interactions between the voice coil and a permanent magnet. The voice coil consists of many coils of wire and is located under the diaphragm. It is held in place by the spider, a frame that supports the coil. The voice coil is surrounded by a strong permanent magnet. Leads, which are attached to the voice coil through the spider, send the voice coil oscillating electrical signals that cause the wire in the coil to have a changing magnetic field. This changing magnetic field “causes the coil to move within the fixed field” of the permanent magnet (Fiore, 2024). Because the coil is attached to the diaphragm, when it moves the diaphragm does too. As the diaphragm vibrates, it increases and decreases pressure on the air (pushing air particles as it moves forward and “pulling” or creating areas of low pressure as it moves backwards, like with the piston), producing sound waves.
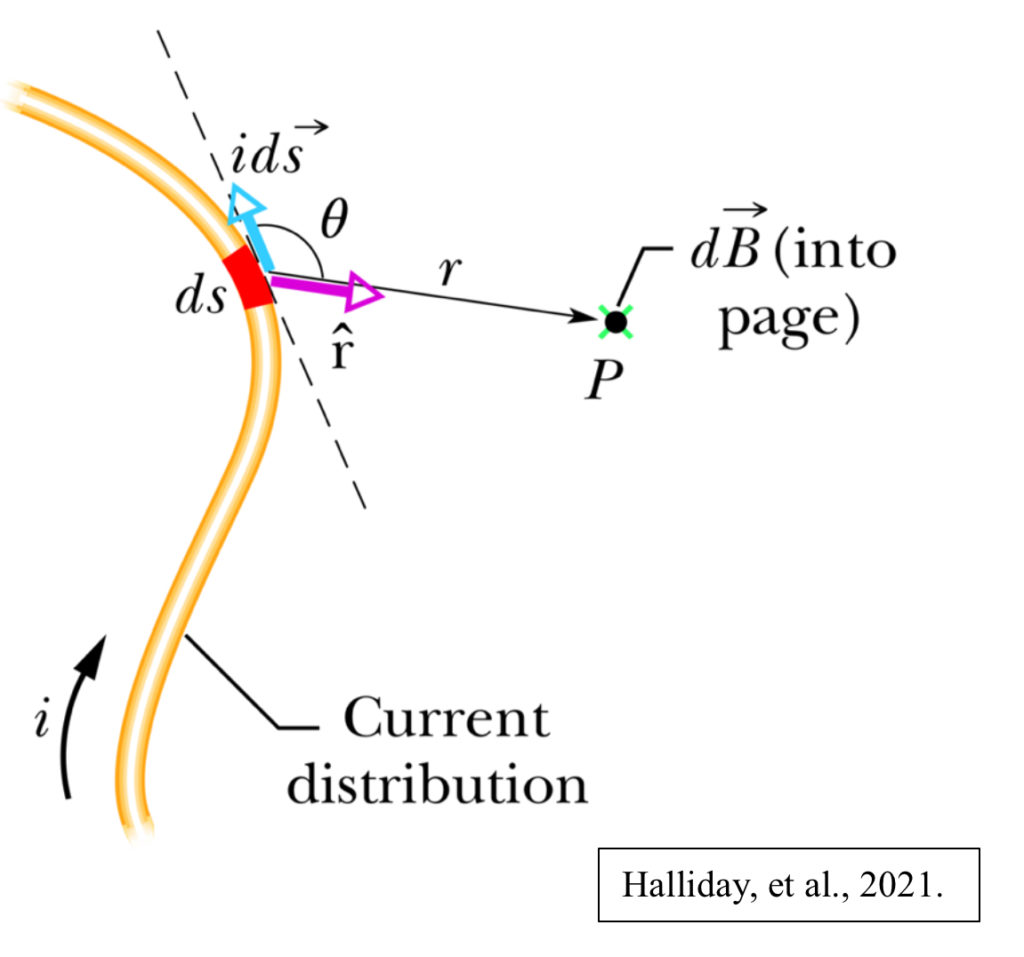
An additional mathematical concept tying into speakers is the law of Biot and Savart, which is used in order to calculate the strength of a magnetic field inside the voice coil. A variation of the law of Biot and Savart gives “the magnitude of the magnetic field at the center of a full circle of current” when B = (µ0i(2π))/(4πR) = (μ0i)/(2R) (Halliday et al. 2021). The law of Biot and Savart is dB = (µ0)/(4π) * (i ds sinθ)/(r2) in scalar form, and dB = (µ0)/(4π) * (i ds x r)/(r2) in vector form (there should be vector hats over dB, and ds and a unit vector hat only over r).
This equation can be derived by applying the magnetic Gauss’s law, the Ampere’s law, Green’s function of a differential operator, and the vector Laplacian (Low, 2024). µ0 is a constant, known as the permeability of free space, and has a value of 4π x 10-7 T * m/A. i represents the direction of the current, which is either positive or negative in amperes. Vector dl is an infinitely small portion of the wire in the same direction as i in meters. Unit vector r is the unit vector from ds to some point P in meters, and r = R. θ is the angle between dl and unit vector r in degrees. Lastly, the net magnetic field at point P is represented by B in teslas (Ling et al., 2016).
Unlike dynamic speakers, electrostatic speakers rely on electrical interactions between thin sheets containing metal. Two thin sheets of metal, also known as grids, sandwich a thin film of plastic, with only a small air gap in between each of the sheets. Both the plastic and grids are charged, and oscillating electrical signals are sent to the grids. This causes the plastic to act as the diaphragm, because the electric signals cause it to vibrate back and forth, allowing the diaphragm to push on the air, producing sound. An advantage of electrostatic speakers over dynamic speakers is their light weight, allowing it to produce higher pitches well. They can also be scaled up to a larger size, and a bigger diaphragm allows the sound to be “less localized”, unlike magnetic speakers, “making the sound seem more natural” (Forinash & Christian, 2024).
The enclosure of a speaker also greatly affects sound quality. Making high-fidelity speakers (speakers that produce good quality sound) necessitates putting the speaker in an enclosed area, and there are several reasons why. For one, a speaker out in the open can cancel out its own sound at the front because the back of the speaker is also producing sound waves. When the diaphragm increases air pressure at the front, there will be a decrease in pressure at the back, and vice versa. Additionally, it is difficult for speakers to produce wavelengths longer than its diameter because there is a poor impedance match with the air, demonstrated by resistance decreasing as the speaker diameter decreases. An enclosure would improve the speaker’s effective size. The enclosure also allows multiple speakers with a large range of frequencies to work together. Because non-enclosed speakers have a diaphragm suspended elastically so they can vibrate, the diaphragm will naturally vibrate the strongest at its resonant frequency, which will warp the sound. This can be solved by utilizing a crossover network, where there are multiple speakers that each produce a specific range of frequencies (Cohen, 1968).
Bibliography:
AHElectronics. (2015). Instructables. https://www.instructables.com/
How-to-make-a-speaker-4/
Cohen, A. (1968). Hi-Fi loudspeakers and enclosures. Hayden Book Company.
Dirks, K., Sharma, M., Podolak, K., & Smith, H. (n.d.). College physics 2e.
https://openstax.org/details/books/college-physics-2e
Fiore, J. (2024). Loudspeakers. LibreTexts Engineering. Retrieved December 8,
2024, from https://eng.libretexts.org/Bookshelves/Electrical_Engineering/
Electronics/Semiconductor_Devices_-_Theory_and_Application_(Fiore)/
08%3A_BJT_Class_A_Power_Amplifiers/8.4%3A_Loudspeakers
Forinash, K., & Christian, W. (2024). Sound: An interactive eBook. Compadre.
Retrieved December 3, 2024, from https://www.compadre.org/books/SoundBook
Halliday, D., Resnick, R., & Walker, J. (2005). Fundamentals of physics (7th
ed., Vol. 1). John Wiley and Sons.
Halliday, D., Resnick, R., & Walker, J. (2021). Fundamentals of physics (12th
ed., Vol. 2). John Wiley and Sons.
Henderson, T. (1996). The speed of sound. The Physics Classroom. Retrieved March
2, 2025, from https://www.physicsclassroom.com/class/sound/lesson-2/
the-speed-of-sound
Ling, S., Moebs, W., & Sanny, J. (2016, October 6). University physics volume 2.
Openstax. Retrieved December 8, 2024, from https://openstax.org/books/
university-physics-volume-2/pages/12-1-the-biot-savart-law
Low, T. (2024, January 1). Derive biot savart’s law from maxwell
equations…[Concepts challenge] [Video]. YouTube. https://www.youtube.com/
watch?v=bXslyzSAhv4
Nave, C. (2017). Speed of sound in various bulk media. HyperPhysics. Retrieved
March 3, 2025, from http://hyperphysics.phy-astr.gsu.edu/hbase/Tables/
Soundv.html
Purves, D., Augustine, G., Fitzpatrick, D., Hall, W., LaMantia, A.-S., McNamara,
J., & White, L. (n.d.). Neuroscience (12th ed.). Purves D, Augustine GJ,
Fitzpatrick D, et al., editors. Neuroscience. 2nd edition. Sunderland (MA):
Sinauer Associates; 2001. The Audible Spectrum. Available from:
https://www.ncbi.nlm.nih.gov/books/NBK10924/#
