By Alondra Caba
Whether it is Pi (π) day, the pursuit of many to memorize thousands upon thousands of digits, or eating celebratory pies in its honor, this irrational number is never short of fame every year. Phi, however, does not fall too far behind. It is best known as the “golden” ratio, and appreciated for its “natural” presence in nature, art, and society. However, is it really as mystical as people believe? The Pythagoreans were horrified at the thought of any irrational numbers, but were their fears reasonable? Though the mathematics behind the golden ratio are relatively simple, its irrationality, so to speak, is something that can be appreciated regardless of any superstitious value or otherwise.
Fibonacci Numbers, Phi, and the Golden Ratio
To understand phi (Φ) and the golden ratio, it is important to first understand the Fibonacci sequence. The Fibonacci sequence is an example, specifically the most popular, of a recursive sequence. A recursive sequence is a series of numbers defined by at least one of its preceding values (Morris., n.d.) Thus, the Fibonacci sequence is a type of recursive sequence where each number in the sequence is a sum of the two values that precede it. Algebraically, it is expressed as FN = F(N-1) + F(N-2). It is important that, though the Fibonacci sequence is standardized by its two starting numbers 0 and 1, the sequence can be achieved with any two starting values. The reason why is because any series of Fibonacci sequences share a vital characteristic: the ratio between sequential values will get closer and closer to the golden ratio, Φ. For example, in the following standard sample of the Fibonacci sequence, the later ratios are closer to 1.618 (the rounded value of phi) than the previous ones:
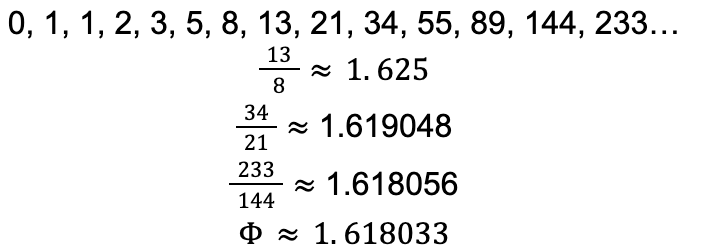
Although the Fibonacci sequence was found to have a relationship with the golden ratio, the history of the golden ratio actually precedes Fibonacci’s numbers. The golden ratio was identified as far back as 300 B.C.E, though not by name. Euclid’s Elements repeatedly highlights the idea of a straight line divided into “extreme and mean ratio” (Heiberg, 2008). His book, which provides proofs and definitions for elementary geometry, provides a geometric visualization of the golden ratio. Euclid claims that a straight line is in extreme and mean ratio when “as the whole is to the greater segment so the greater (segment is) to the lesser” (2008). In other words, given a straight line ABC segmented at point B where AC represents the whole, AB is the longer part, and BC is the shorter part; the ratio of AC to AB is equal to the ratio of AB to BC. Phi is, essentially, the relationship between the line segments when split into this special “extreme and mean ratio.”
Basic Formula of Phi
Euclid’s Elements provides an accurate geometric representation of the golden ratio, but it can be expressed algebraically as well. Assuming that the greater and lesser segments are instead defined as values x and y, x and y are in the golden ratio when the following equation is true:
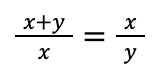
Thus, the ratio is algebraically defined as the following equation:
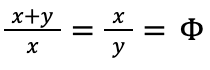
However, this equation does not give an exact value of Φ. Rather, it just shows the conditions that must be met to fulfill the ratio. A solution to this is to set y equal to 1, creating a unit ratio that is still equivalent to the original equation. This way, y = 1, and we can say that x = Φ (Choi et al. 2023). The new equation is now
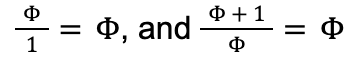
Solving for can be done with algebra and creating the quadratic equation Φ2 – Φ – 1 = 0. With the quadratic formula, we can find the following solutions:
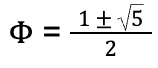
Of the two solutions, the golden ratio, , is the positive root. Keeping in mind Euclid’s geometric representations, it is impossible to have a “negative” line segment. Thus, it’s vital that the equation is the positive solution. Therefore:
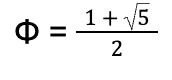
Is it Superstition or Science?
Visually, the golden ratio is so special because the sequence creates a spiral image. The best example of this is the “golden rectangle” in which the side lengths of the rectangle are in the golden ratio. This is done by splitting the rectangle into a square and another smaller rectangle. Within this smaller rectangle, another square can be placed, and the cycle continues to make similar rectangles all in the golden ratio. Then, arcs can be drawn through each square to create the spiral.
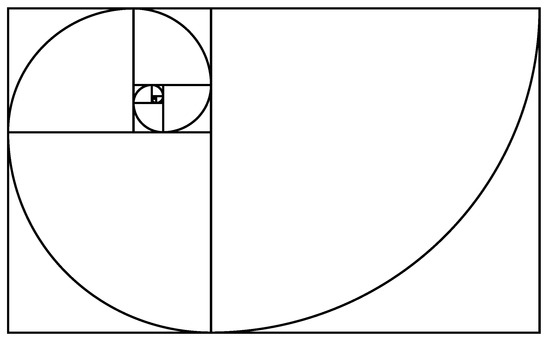
(Marples & Williams, 2022).
However, though spirals are common patterns in nature, this does not grant a “mystical” power to the golden ratio. Rather, the mathematical value of the golden ratio is something that can be utilized and applied in different disciplines. For example, petal and seed growth on different species of flowers can be found to follow closely in relation to Fibonacci numbers. Specifically, the seeds in the center of sunflowers are shown to follow spiral patterns in two opposing directions. Counting these seeds in each direction shows a relationship approximate to the golden ratio between the opposing spirals (Choi et al., 2023). Visually, the golden ratio is pleasing and oddly satisfying, but human appreciation for spirals does not exactly mean there is true “power” behind the ratio. Thus, it is more likely that the golden ratio may not have any metaphysical value other than what society attributes to it.
However, it is acceptable if the ratio does not have any mysterious power in nature. What makes the golden ratio special is not the myths surrounding it. Rather, it is the ability to find beauty in a number, one that was feared by the Pythagoreans centuries ago. To make sense of the irrational is something unique, both aesthetically and also theoretically. Its naturally occurring presence in nature gives scientists a value to reference when finding similar patterns.
Bibliography:
Choi, J. , Atena, A. and Tekalign, W. (2023) The Most Irrational Number that Shows up Everywhere: The Golden Ratio. Journal of Applied Mathematics and Physics, 11, 1185-1193
Heiberg, J. L. (2008). Euclid’s Elements of Geometry (R. Fitzpatrick, Ed. & Trans.). https://farside.ph.utexas.edu/Books/Euclid/Elements.pdf (Original work published 1883-1885).
Mann, A. (2019, November 25). Phi: The Golden Ratio. Live Science. https://www.livescience.com/37704-phi-golden-ratio.html
Marples, C. R. & Williams, P. M. (2022). The Golden Ratio in Nature: A Tour Across Length Scales. Symmetry, 14(10), 2059. https://doi.org/10.3390/sym14102059
Meisner, G. (2012, May 13). History of The Golden Ratio. GoldenNumber. https://www.goldennumber.net/golden-ratio-history/
Morris, J. (n.d.) Recursively Defined Sequences. LibreTexts Mathematics, https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/Combinatorics_(Morris)/02%3A_Enumeration/06%3A_Induction_and_Recursion/6.01%3A_Recursively-Defined_Sequences
Naini, F. B. (2024). The Golden Ratio–Dispelling The Myth. Maxillofacial Plastic and Reconstructive Surgery, 46(2), https://doi.org/10.1186/s40902-024-00411-2
Yearsley E. S. (2022). Nature and Math: The Fibonacci Sequence in Nature. Johnson Museum of Art, https://museum.cornell.edu/nature-and-math-the-fibonacci-sequence/
